春分日除了“竖蛋”还能做什么？ 一起来做埃拉托斯特尼实验估测地球周长吧！

翻开任何一本现代的入门科普书或进行网络搜索，我们都能轻松的查到地球的直径与周长的精确数据：平均直径约为12742千米，赤道周长约为40076千米，这是利用人造卫星等先进工具测量出来的。那在科技并不发达的古代，人们是如何知道地球周长的呢？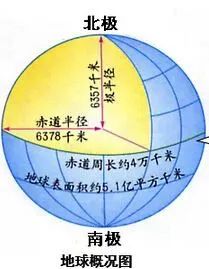

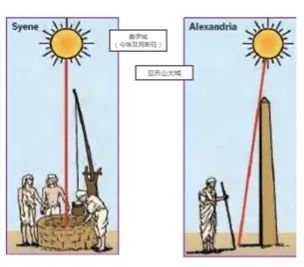
人类最早对地球直径与周长的测量是在公元前200多年，也就是中国秦始皇那个时代。当时古希腊的数学家、地理学家、天文学家、著名的埃及亚历山大图书馆馆长埃拉托斯特尼（Eratosthenes，公元前280～前190年）利用巧妙的测量方法粗略测量了地球的大小。据说当时在亚历山大港（Alexandria）以南与之几乎同经度的塞伊尼（Syene，大致相当于现在埃及南部的阿斯旺地区）有一口很深的竖井，每到夏至日（即每年6月21或22日，这天太阳直射北回归线）这天的正午，太阳光能够一直照射到井的最底部。

也就是说，在那个地方夏至日正午太阳位于正天顶，其入射角为0度。然而在位于埃及北部尼罗河三角洲地中海沿岸的亚历山大港，夏至日正午时太阳却无法直射地面，因此埃拉托斯特尼使用一根高塔（如方尖碑）采用测量影子长度的方法来测量太阳照射的角度。使用简单的几何学知识，他测出太阳光的入射角为7.2度。

如果接受地球是球形的观点（这已被之前的科学家利用月食时月球被遮掩边缘的形状等证据普遍证实了），那么这7.2度的差值就应该是亚历山大港与塞伊尼两地所对应的地面弧距（如图所示），大致相当于360度圆周的1/50。他询问了往返于两地的驼队商人，得到了大致的旅行所需时间，按照骆驼平均的行进速度，粗略估计出两地的距离大致为5000“斯台地亚”（Stadia，当时的长度单位，按照希腊制大致相当于155米），由此他计算出地球的周长大致为5000✕50=25万斯台地亚，即约为3.9万千米，真的与现代测量的精确数值相差无几呢！

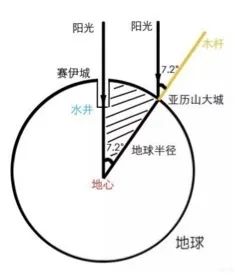
这就是著名的埃拉托斯特尼实验（Eratosthenes Experiment）。当然我们现在要开展类似的测量地球周长的实验，也不一定要找像塞伊尼那样特殊的地方（正处于北回归线上，因此夏至日正午太阳直射），也不一定需要等到夏至。

每年国际上都将组织在春分日那天（今年为3月20-21日）的“埃拉托斯特尼实验”联测活动（官方活动网址为：http://eratosthenes.ea.gr），利用测量比较处于同一经度不同地点春分日当地正午的日影长度，甚至可以通过单地测量值与同经度虚拟赤道上观测点的比较，就可以计算地球的周长。活动号召世界各地的学校积极注册参与，测量并上报数据。同时，可以拍下你们做实验的精彩照片，参加照片竞赛（Photo Contest）哦~

测量方法比较简单，通过几何三角知识利用影长测出太阳入射角θ（θ= arctan（影长/杆长）），与同经度另一地点的入射角比较，算出两地间的弧距Δθ。利用网络地图（如百度地图）粗略测出两地间的距离d。则：

地球周长≈两地距离d ✕ 360° / 两地弧距Δθ --- 式1。

如果没有找到与你的经度近似的另一个观测点（若两地经度不完全相同，可将对方观测地位置同纬度平移至你的经度处再测距即可），也可以与（同经度）虚拟的赤道地区观测点进行比较：由于春分日太阳直射赤道（赤道地正午太阳入射角为0），因此你处与同经度赤道地点间的弧距就是在你处测量所得的太阳入射角θ，同样利用网络地图测出两地间的距离d。则：

地球周长≈两地距离d ✕ 360° / 太阳入射角θ --- 式2 。

注意：式1对所有测量日期（不一定是春分日）都成立，而式2只对春分日当天成立。

另外还要注意测量时间为观测地当地时间正午（local noon），而并非所在地平常所使用的区时（如北京时间），需要进行简单换算。可以在正午12点附近多测几次，取最短影长的数值代入计算（想想为什么？），或是利用Stellarium软件等模拟演示（太阳正南180度时刻）。

大家是不是心动了呢？在春分日，除了玩一玩“竖蛋”游戏外，请一起来做埃拉托斯特尼实验吧！可以把你的测量结果和粗略估算的地球周长留言告诉我们哦~

编辑审核：逺才老师

山东大学威海天文台（暨威海市天文台）

山东大学空间科学研究院

山东天文学会

2022.3.20

本文链接：https://www.bjjcc.cn/kepu/44119.html，文章来源：科普之家，作者：山东天文科普教育，版权归作者所有，如需转载请注明来源和作者，否则将追究法律责任！